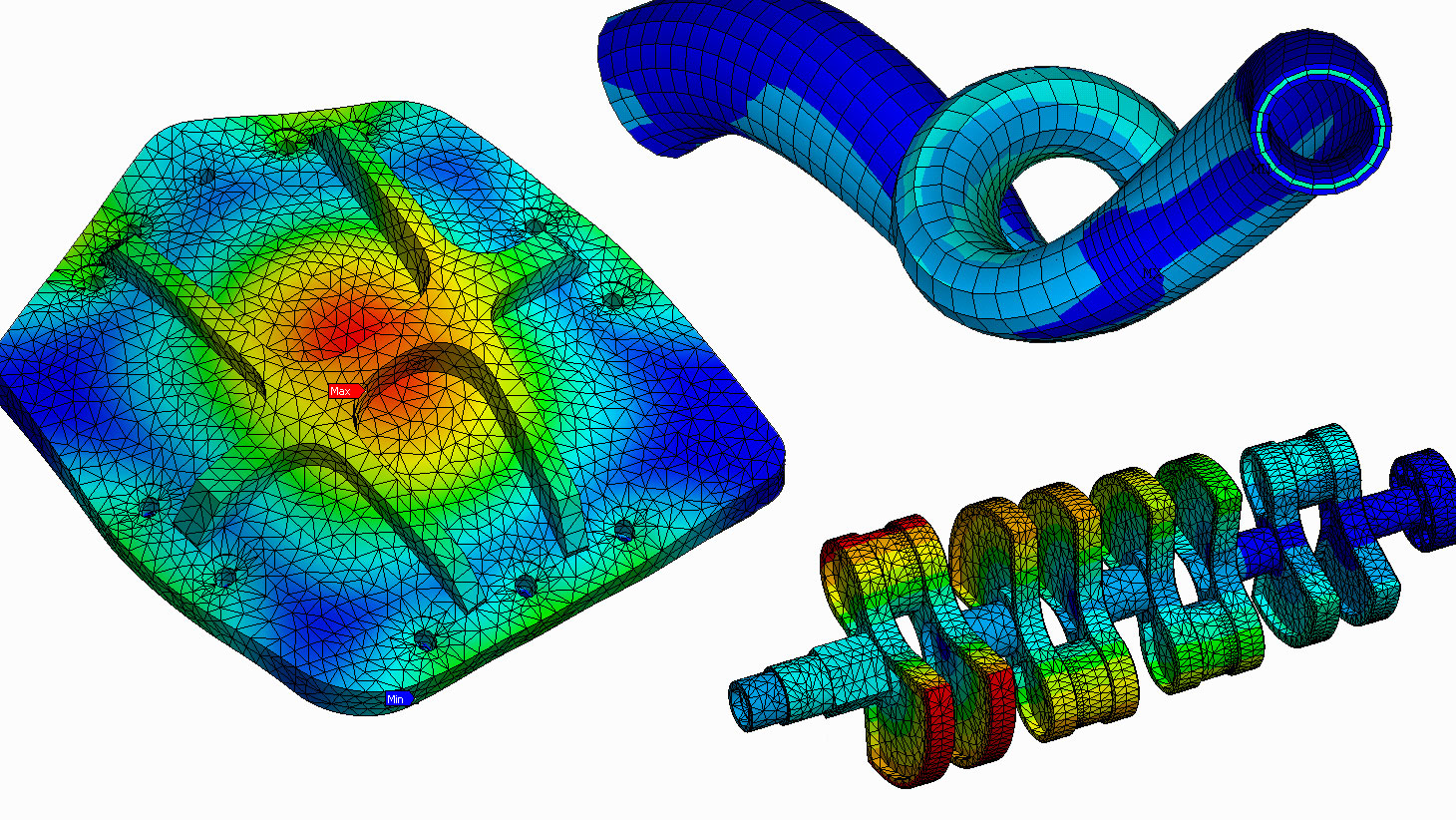
¿Método numérico, analítico y experimental: concurrentes o complementarios en la ingeniería?
Actualmente, las empresas de ingeniería enfrentan a varios desafíos durante sus proyectos. Todo el proceso asociado al desarrollo de un equipo, producto o estructura debe presentar un buen balance de factores cruciales, como calidad, costo y tiempo, y el escenario observado en los días de hoy trae diversas dificultades para que se alcance este equilibrio. Por ejemplo, la complejidad de los productos es cada vez mayor, los recursos (tanto humanos como de materia prima) son más escasos y los plazos para la conclusión de los proyectos y el lanzamiento de productos más cortos. Ante estos desafíos, la simulación numérica se presenta como una herramienta de gran utilidad, que presenta varios beneficios para la solución de problemas de ingeniería, aliada a los métodos tradicionales.
En general, la resolución de problemas de ingeniería puede ser realizada según tres enfoques generales: Métodos Analíticos, Métodos Experimentales y Métodos Numéricos, presentados abajo.
Los métodos analíticos representan soluciones basadas en fórmulas matemáticas, desarrolladas generalmente de forma manual, en las que se definen variables de entrada para el cálculo de una o más variables de salida. Algunos ejemplos consisten de ecuaciones elementales disponibles en la literatura de ingeniería o procedimientos descritos en normas técnicas de organizaciones y clasificadoras como ASME, ASTM y DNV. Se trata de una metodología simple, en general de bajo costo y complejidad, que proporciona una respuesta rápida y directa después de la solución de estas ecuaciones.
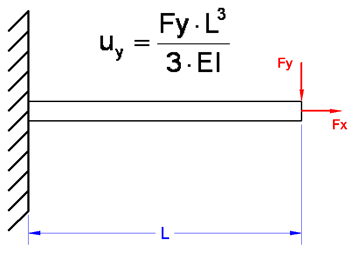
Ejemplo de cálculo analítico
Sin embargo, cálculos analíticos presentan aspectos que limitan su aplicabilidad para casos prácticos. Por ejemplo, las ecuaciones generalmente contemplan características físicas y de operación relativamente idealizadas, muy simplificadas si se comparan con lo que se observa en la realidad, o se restringen a las condiciones específicas previstas en el cálculo. De esta forma, los resultados obtenidos por estos métodos pueden presentar una desviación significativa en relación al producto real, lo que ocasiona problemas como sobre-dimensionamiento, factores de seguridad demasiado elevados y, consecuentemente, mayores costos de producción, además de no proporcionar un entendimiento detallado del comportamiento del objeto en estudio.
Los métodos experimentales dependen de los prototipos físicos del equipo o producto, construidos a escala real o reducida, que se someten a un ensayo que representa una determinada condición de operación. La prueba de colisión de un automóvil o el estudio aerodinámico de una aeronave en el túnel de viento son ejemplos clásicos de métodos experimentales que pueden ser destructivos o no destructivos. La calidad de los resultados obtenidos en este tipo de enfoque típicamente es alta, ya que la evaluación se realiza en un prototipo que representa fielmente las características físicas y constructivas del proyecto, cuando sujeta a las cargas reales de operación. Además, en estos ensayos típicamente se utilizan dispositivos y sistemas para medición de datos, garantizando una comprensión detallada de los fenómenos de interés.

Prueba experimental con prototipo físico
Sin embargo, el desarrollo de pruebas experimentales requiere una mayor inversión, no sólo por el coste de construcción del prototipo, sino también para poner a disposición la infraestructura necesaria para los ensayos. Además, el proceso de desarrollo puede requerir la realización de múltiples iteraciones hasta alcanzar un diseño adecuado, con impacto directo en el tiempo y costo del proyecto. Esto se muestra más significativo en situaciones donde los ensayos son destructivos y / o requieren pruebas físicas de larga duración (como fatiga, por ejemplo). Con ello, el enfoque experimental se caracteriza por costos elevados y plazos extensos, impactando en el proceso productivo.
Por último, en la solución por medio de Métodos Numéricos se desarrolla un prototipo virtual del producto de interés, representado por un sistema de ecuaciones fundamentadas en una teoría matemática, como Método de Elementos Finitos (MEF), por ejemplo. Este modelo puede ser construido directamente en software comercial de simulación numérica o incluso por medio de un código de programación propio desarrollado por el ingeniero. Se trata de un enfoque que equilibra los puntos positivos de las demás: aunque requiere una inversión razonablemente superior al método analítico (debido a la infraestructura de hardware, licencias de software y entrenamiento de los usuarios), el costo es significativamente inferior a un ensayo experimental; a su vez, a pesar de que el modelado numérico considera hipótesis simplificadoras en relación a la realidad, es posible obtener una representación muy próxima al comportamiento de un prototipo físico.

Simulación numérica en software commercial
Además, cabe resaltar que el uso del método numérico presenta una serie de características destacadas, que la hacen una solución extremadamente versátil y eficiente para el desarrollo de proyectos de ingeniería. Por ejemplo, los softwares comerciales permiten la importación directa de geometrías desarrolladas en plataformas de CAD (Computer Aided Design) tridimensional, ampliamente usadas en la etapa de proyecto, auxiliando la etapa de preprocesamiento. Otra ventaja es la facilidad para parametrización de los modelos numéricos, lo que posibilita la mejor comprensión de cómo las diferentes variables del proyecto influencian los resultados, la evaluación de diferentes condiciones de diseño y el desarrollo de una configuración optimizada, que atienda a todos los criterios de diseño seguridad exigidos y proporcione la mejora del producto.
Es interesante destacar que la utilización de Métodos Numéricos para la solución de problemas de ingeniería es relativamente reciente si se compara con los demás enfoques tradicionales. Esto se debe al hecho de que, en la época de su surgimiento, el uso de simulación numérica presentaba diversos desafíos que limitaban su aplicabilidad para la solución de problemas de ingeniería con la rapidez exigida por la industria. En este momento inicial, el desarrollo de un análisis numérico era complejo, con un alto tiempo de implementación, influenciado en gran parte por las limitaciones de recursos de hardware y software. Se suma a ello la escasez en la época de profesionales con conocimiento teórico y experiencia en la utilización de los métodos numéricos asociados, muchas veces limitándolos a la investigación científica y al medio académico.
Sin embargo, es posible observar que en los últimos años estos desafíos han sido superados. El significativo avance de la informática, con computadoras de alto rendimiento, posibilitó la mejora de los softwares de simulación numérica, hoy más robustos y capaces de lidiar con problemas físicamente mayores y más complejos. Estas herramientas también incorporaron interfaces más simples y ágiles, haciendo su operación más rápida y con mayor capacidad de automatización de ciertas tareas (como realización de análisis paramétricos, por ejemplo). Cabe resaltar también que actualmente existe una mayor difusión del conocimiento teórico de los métodos matemáticos empleados, de forma que más ingenieros tienen acceso a sus conceptos fundamentales en cursos de postgrado e incluso de graduación, o incluso a través de capacitación interna en las empresas.
El uso de simulación numérica tiene varios puntos positivos, como se ha señalado anteriormente. Sin embargo, no debe considerarse como sustituto de los métodos tradicionales, que son igualmente fundamentales para la solución de problemas de ingeniería. Por ejemplo, procedimientos analíticos basados en normas son imprescindibles para la certificación de equipos y procesos, así como ciertas aplicaciones exigen la realización de ensayos experimentales para la aprobación del proyecto. Además, las informaciones obtenidas en experimentos e incluso en cálculos analíticos sirven como referencia para la calibración de parámetros de una simulación numérica, asegurando así una representación fiel del fenómeno físico de interés. Un ejemplo típico es la realización de un ensayo uniaxial de tracción, que permite el levantamiento de la curva tensión x deformación del material, que puede ser usada en el análisis para caracterizar la respuesta estructural del material.
De esta forma, la simulación numérica debe ser vista como un enfoque complementario a los métodos analítico y experimental, aportando varios beneficios para el proyecto, y proporcionando a los ingenieros más recursos para lograr un buen balance de la calidad, el tiempo y el costo de sus productos, equipos y procesos.

