Método de los elementos finitos: ¿qué es?
La simulación computacional se utiliza ampliamente en las empresas para hacer análisis y mejorar la calidad de los productos y proyectos. La mayoría de estos análisis se llevan a cabo mediante uso de softwares que utilizan el Método de Elementos Finitos, lo cual permite obtener respuestas para numerosos problemas de ingeniería.
¿Cómo funciona el método?
La geometría de la pieza, sometida a cargas y restricciones, se subdivide en partes más pequeñas, conocidas como “elementos”, que representan el dominio continuo del problema. La división de la geometría en pequeños elementos resuelve un problema complejo, al subdividirlo en problemas más simples, lo que permite a la computadora hacer las tareas con eficiencia.
El método propone que un número infinito de variables desconocidas, sean sustituidas por un número limitado de elementos de comportamiento bien definido. Esas divisiones pueden tener diferentes formas, tales como triangular, cuadrangular, entre otros, dependiendo del tipo y tamaño del problema. Como el número de elementos es limitado, son llamados de “elementos finitos” – palabra que da nombre al método.
Los elementos finitos están conectados entre sí por puntos, que se llaman nodos o puntos nodales. Al conjunto de todos estos ítems – elementos y nodos – se lo denomina malla. Debido a las subdivisiones de la geometría, las ecuaciones matemáticas que rigen el comportamiento físico no se resolverán de una manera exacta, sino aproximada por este método numérico. La precisión de los Métodos dos Elementos Finitos depende de la cantidad de nodos y elementos, del tamaño y de los tipos de elementos de la malla. Por lo tanto, cuanto menor sea el tamaño y mayor el número de elementos en una malla, más precisos serán los resultados de las análisis.
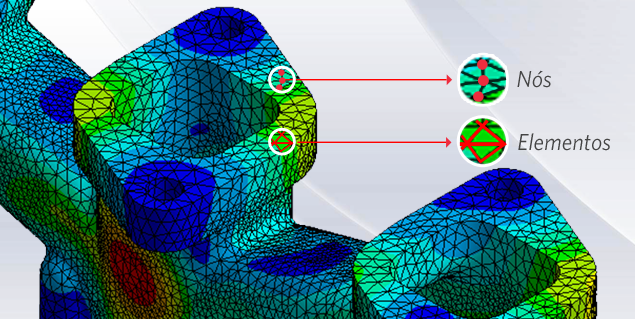
Nodos y elementos de una malla
Los softwares de simulación computacional están evolucionando y mejorando los análisis con base en el método, promoviendo la mejora de selección de tipos y generación de malla de elementos, las técnicas de modelado, criterios de aceptación, los errores y la presentación de los resultados, permitiendo la utilización más fácil de las herramientas. Por lo tanto, el conocimiento de los fundamentos del método es necesario para que juntamente con el dominio del software se desarrollen las mejores prácticas para la aplicación de éste poderoso recurso en el desarrollo y evaluación de productos y proyectos.
Aplicación del Método dos Elementos Finitos
El método puede ser aplicado en la resolución y diagnóstico de problemas de análisis estructural pala la obtención de desplazamientos, deformaciones y tensiones, también permite representar diferentes escenarios y evaluar el rendimiento de productos con aplicación de criterios de resistencia, rigidez o fatiga. También las variaciones del método de los elementos finitos permiten hacer análisis térmico, acústico, dinámico, electromagnético y de flujos de los casos más simples de comportamiento linear al no linear, como cuando se tienen grandes desplazamientos o contacto entre las partes de un conjunto.

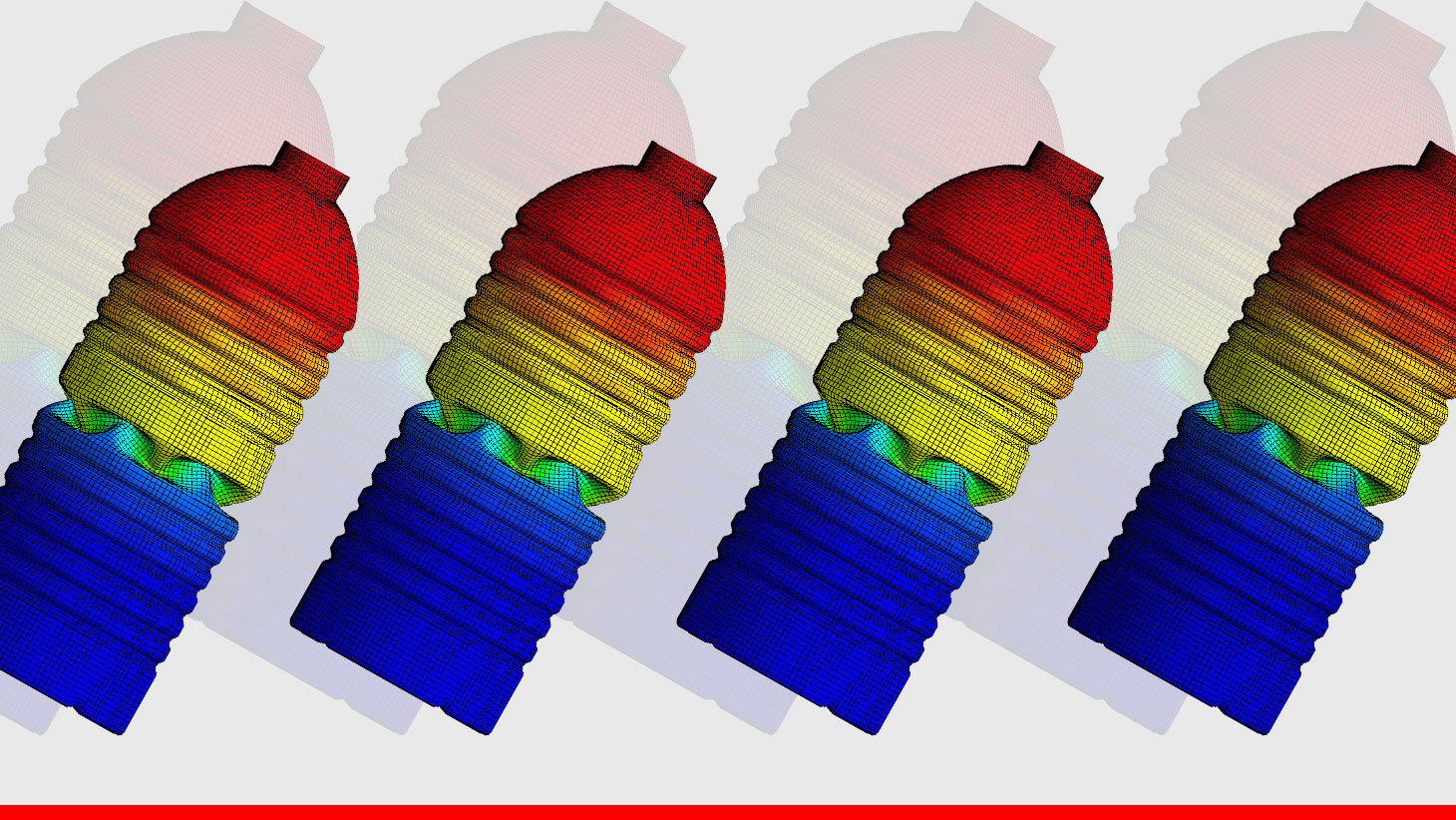
Simulación de producto realizada con ayuda del análisis de elementos finitos
Es posible con las tecnologías actuales hacer integraciones con los softwares utilizados en el desarrollo de representación geométrica – conocidos como CAD (Computer-Aided Design) – con los sistemas basados en el Método dos Elementos Finitos – llamados de CAE (Computer-Aided Engineering). Esa integración permite lograr los mejores resultados con un análisis más eficiente y ágil.

