Método numérico, analítico e experimental: concorrentes ou complementares na engenharia?
Atualmente, empresas de engenharia se deparam com vários desafios durante seus projetos. Todo o processo associado ao desenvolvimento de um equipamento, produto ou estrutura deve apresentar um bom balanceamento de fatores cruciais, como qualidade, custo e tempo, e o cenário observado nos dias de hoje traz diversas dificuldades para que se atinja este equilíbrio. Por exemplo, a complexidade dos produtos é cada vez maior, os recursos (tanto humanos como de matéria-prima) são mais escassos e os prazos para a conclusão dos projetos e lançamento de produtos mais curtos. Diante destes desafios, a simulação numérica se apresenta como uma ferramenta de grande utilidade, que apresenta vários benefícios para a solução de problemas de engenharia, aliada aos métodos tradicionais.
De uma forma geral, a resolução de problemas de engenharia pode ser realizada segundo três abordagens gerais: Métodos Analíticos, Métodos Experimentais e Métodos Numéricos, apresentadas a seguir.
Métodos Analíticos representam soluções baseadas em fórmulas matemáticas, desenvolvidas geralmente de forma manual, em que são definidas variáveis de entrada para o cálculo de uma ou mais variáveis de saída. Alguns exemplos consistem de equações elementares disponíveis em literatura de Engenharia ou procedimentos descritos em normas técnicas de organizações e classificadoras como ASME, ASTM e DNV. Trata-se de uma metodologia simples, em geral de baixo custo e complexidade, que proporciona uma resposta rápida e direta após a solução destas equações.
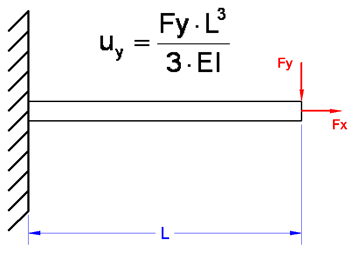
Exemplo de cálculo analítico
Entretanto, cálculos analíticos apresentam aspectos que limitam a sua aplicabilidade para casos práticos. Por exemplo, as equações geralmente contemplam características físicas e de operação relativamente idealizadas, muito simplificadas se comparadas com o que se observa na realidade, ou são restritas às condições específicas previstas no cálculo. Desta forma, os resultados obtidos por estes métodos podem apresentar um desvio significativo em relação ao produto real, o que ocasiona problemas como sobre-dimensionamento, fatores de segurança demasiadamente elevados e, consequentemente, maiores custos de produção, além de não proporcionarem um entendimento detalhado do comportamento do objeto em estudo.
Métodos Experimentais dependem de protótipos físicos do equipamento ou produto, construídos em escala real ou reduzida, que são submetidos a um ensaio que representa uma determinada condição de operação. O teste de colisão de um automóvel ou o estudo aerodinâmico uma aeronave em túnel de vento são exemplos clássicos de métodos experimentais, que podem ser destrutivos ou não-destrutivos. A qualidade dos resultados obtidos neste tipo de abordagem tipicamente é alta, uma vez que a avaliação é realizada em um protótipo que representa fielmente as características físicas e construtivas do projeto, quando sujeita aos carregamentos reais de operação. Além disso, nestes ensaios tipicamente são usados dispositivos e sistemas para aferição de dados, garantido uma compreensão detalhada de fenômenos de interesse.

Teste experimental com protótipo físico
Porém, o desenvolvimento de testes experimentais exige um maior investimento, não apenas por conta do custo de construção do protótipo, mas também para disponibilizar a infraestrutura necessária para os ensaios. Além disso, o processo de desenvolvimento pode exigir a realização de múltiplas iterações até atingir um design adequado, com impacto direto no tempo e custo do projeto. Isso se mostra mais significativo em situações onde os ensaios sejam destrutivos e/ou exijam testes físicos de longa duração (como fadiga, por exemplo). Com isso, a abordagem experimental se caracteriza por custos elevados e prazos extensos, impactando no processo produtivo.
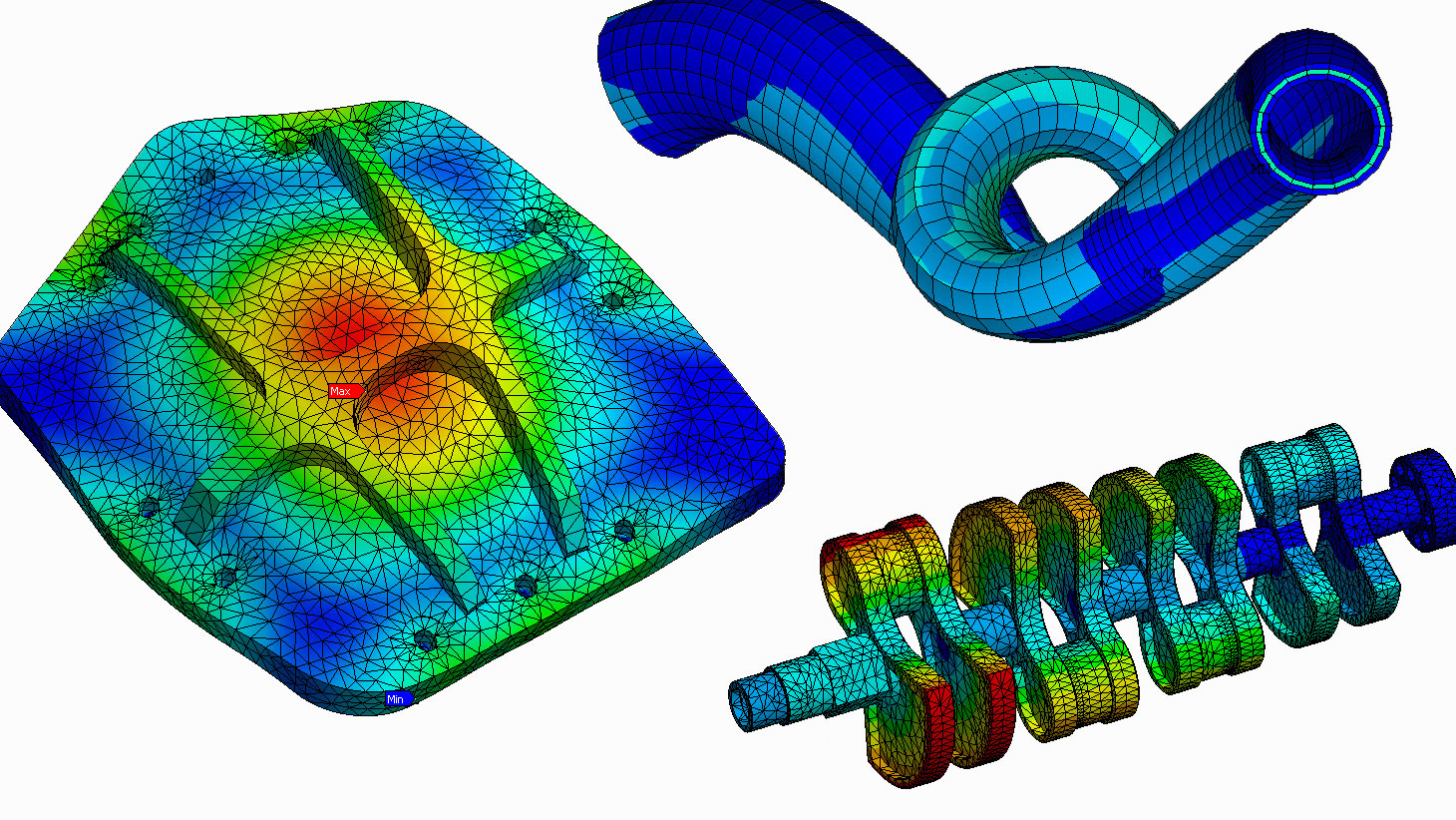
Por fim, na solução por meio de Métodos Numéricos é desenvolvido um protótipo virtual do produto de interesse, representado por um sistema de equações fundamentadas em uma teoria matemática, como Método de Elementos Finitos (MEF), por exemplo. Este modelo pode ser construído diretamente em softwares comerciais de simulação numérica ou mesmo por meio de um código de programação próprio desenvolvido pelo engenheiro. Trata-se de uma abordagem que equilibra os pontos positivos das demais: embora demande um investimento razoavelmente superior ao método analítico (por conta de infraestrutura de hardware, licenças de software e treinamento dos usuários), o custo é significativamente inferior a um ensaio experimental; por sua vez, apesar da modelagem numérica considerar hipóteses simplificadoras em relação à realidade, é possível obter uma representação muito próxima ao comportamento de um protótipo físico.

Simulação numérica em software comercial
Além disso, cabe ressaltar que o uso do método numérico apresenta uma série de características de destaque, que a tornam uma solução extremamente versátil e eficiente para o desenvolvimento de projetos de engenharia. Por exemplo, os softwares comerciais permitem a importação direta de geometrias desenvolvidas em plataformas de CAD (Computer Aided Design) tridimensional, largamente usadas na etapa de projeto, auxiliando a etapa de pré-processamento. Outra vantagem é a facilidade para parametrização dos modelos numéricos, o que possibilita a melhor compreensão de como as diferentes variáveis do projeto influenciam os resultados, a avaliação de diferentes condições de projeto e o desenvolvimento de uma configuração otimizada, que atenda a todos os critérios de segurança exigidos e proporcione a melhoria do produto.
É interessante destacar que a utilização de Métodos Numéricos para a solução de problemas de engenharia é relativamente recente se comparada com as demais abordagens tradicionais. Isso se deve ao fato de que, na época de seu surgimento, o uso de simulação numérica apresentava diversos desafios que limitavam a sua aplicabilidade para a solução de problemas de engenharia com a rapidez exigida pela indústria. Neste momento inicial, o desenvolvimento de uma análise numérica era complexo, com elevado tempo para implementação, influenciado em grande parte pelas limitações de recursos de hardware e software. Soma-se a isso a escassez na época de profissionais com conhecimento teórico e experiência na utilização dos métodos numéricos associados, muitas vezes limitando-os à pesquisa científica e ao meio acadêmico.
Entretanto, é possível observar que nos últimos anos tais desafios foram superados. O significativo avanço da informática, com computadores de alto desempenho, possibilitou a melhoria dos softwares de simulação numérica, hoje mais robustos e capazes de lidar com problemas fisicamente maiores e mais complexos. Estas ferramentas também incorporaram interfaces mais simples e ágeis, tornando sua operação mais rápida e com maior capacidade de automação de certas tarefas (como realização de análises paramétricas, por exemplo). Cabe ressaltar também que atualmente existe uma maior difusão do conhecimento teórico dos métodos matemáticos empregados, de forma que mais engenheiros têm acesso aos seus conceitos fundamentais em cursos pós-graduação e mesmo de graduação, ou mesmo através de capacitação interna nas empresas.
O uso de simulação numérica possui vários pontos positivos, como destacados acima. Entretanto, ela não deve ser considerada como substituta dos métodos tradicionais, que são igualmente fundamentais para a solução de problemas de engenharia. Por exemplo, procedimentos analíticos baseados em normas são imprescindíveis para a certificação de equipamentos e processos, assim como certas aplicações exigem a realização de ensaios experimentais para a aprovação do projeto. Além disso, informações obtidas em experimentos e mesmo em cálculos analíticos servem como referência para a calibração de parâmetros de uma simulação numérica, assegurando assim uma representação fiel do fenômeno físico de interesse. Um exemplo típico é a realização de um ensaio uniaxial de tração, que permite o levantamento da curva tensão x deformação do material, que pode ser usada na análise para caracterizar a resposta estrutural do material.
Desta forma, a simulação numérica deve ser vista como uma abordagem complementar aos métodos analítico e experimental, trazendo vários benefícios para o projeto, e proporcionando aos engenheiros mais recursos para atingir um bom balanceamento da qualidade, tempo e custo de seus produtos, equipamentos e processos.

