
Métodos numéricos para simulação na engenharia
Problemas de engenharia podem ser resolvidos através de diferentes metodologias, sendo que a solução por métodos numéricos proporciona uma série de pontos positivos que colaboram para uma melhor compreensão dos fenômenos com um bom balanceamento entre tempo, custo e qualidade.
Os métodos numéricos são aplicações de algoritmos pelas quais é possível formular e resolver problemas matemáticos usando operações aritméticas menos complexas. Estes também são conhecidos como métodos indiretos. A análise numérica idealiza e concebe métodos para “aprovar” de forma eficiente as soluções de problemas expressados matematicamente. O objetivo principal da análise numérica é encontrar soluções “aproximadas” para problemas complexos.
Um algoritmo é um grupo finito de operações organizadas e ordenadas que permite resolver um certo problema. Trata-se de uma série de instruções ou regras estabelecidas que, por meio de uma sucessão de etapas, permitem aproximar o resultado real.
A análise numérica é o estudo de algoritmos que busca resultados numéricos de problemas das mais diferentes áreas do conhecimento humano, modelados matematicamente. Em geral, os algoritmos de métodos numéricos se dividem em diretos, recursivos e iterativos. Por exemplo, os iterativos apresentam uma sucessão de passos que converge ou não para o valor aproximado da solução exata. É objetivo da análise numérica encontrar sucessões que aproximem os valores exatos com um número mínimo de operações elementares.
Embora a análise numérica tenha sido concebida antes dos computadores, correntemente o assunto se relaciona a uma interdisciplinaridade entre a matemática e a tecnologia da informação. Também é muito referido na disciplina de cálculo numérico.
As descrições aqui apresentadas são simplificadas e objetivam fazer com que o leitor entenda os fundamentos dos métodos, suas diferenças e principais aplicações. São eles:
Método dos Elementos Finitos (FEM)
O método dos elementos finitos (FEM – Finite Element Method) é um método numérico para resolver problemas de engenharia e física matemática. É aplicável para diferentes disciplinas da engenharia como estrutural, térmica e eletromagnética.
É um método numérico que ultrapassa os limites dos problemas que se resolvem com soluções analíticas, sendo adequado para tratar problemas com geometrias, carregamentos e propriedades de materiais complexos.
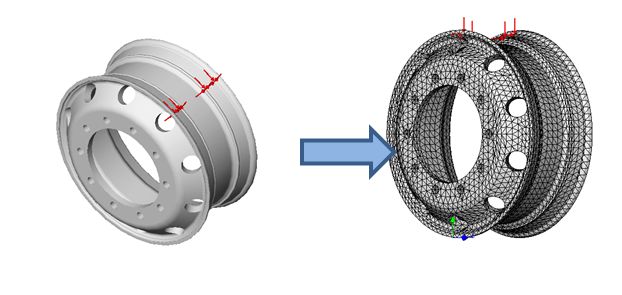
Considere um domínio, por exemplo, a geometria do objeto de estudo. Este domínio será considerado contínuo. Este contínuo é dividido num número discreto de pequenos corpos com formato específico denominados elementos finitos, e interconectados por pontos comuns denominados pontos nodais ou nós.

O procedimento de discretização (a divisão do contínuo em partes menores), equacionamento e cálculo é adequado para a programação e posterior uso em computadores, o que o tornou muito popular e útil para diferentes indústrias. Em resumo, a divisão da geometria em elementos finitos permite resolver um problema complexo, subdividindo-o em problemas mais simples, o que possibilita ao computador realizar com eficiência estas tarefas.
O método dos elementos finitos resolve diferentes problemas que são equacionados e reduzidos a sistemas de equações diferenciais. Por exemplo, considerando-se estruturas chega-se a uma equação, dita equação do movimento, que resume o equilíbrio entre esforços internos de uma estrutura (força inercial, força de amortecimento e força elástica) e uma força externa. Se o problema é estático ou quase estático, considera-se apenas o equilíbrio entre esforços internos elásticos e os esforços externos.
Veja como utilizar o método dos elementos finitos para análises de subestações e demais instalações complexas no webinar Análise de subestações via simulação numérica.
Examine-se um problema simples estático, para entendimento, cujos fundamentos serão aplicados para solução pelo método dos elementos finitos.
Em 1660 Robert Hooke observou e descreveu a chamada lei da Elasticidade, que leva seu nome: a Lei de Hooke. Descreve que a variação da tensão com a extensão numa mola é linear.
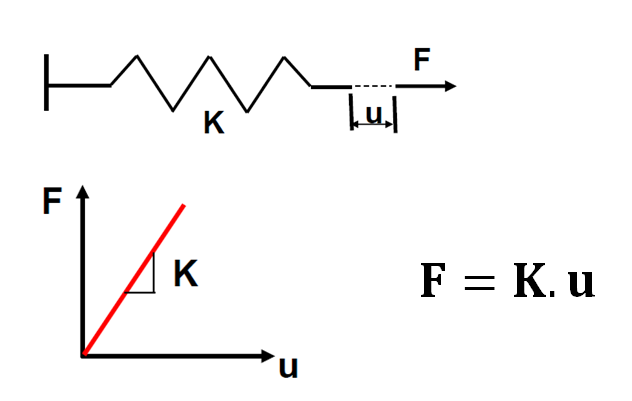
Figura 1: Relação (Lei de Hooke) entre esforço externo (F), rigidez (K) e deslocamento (u). K.u representa o esforço interno.
Num problema onde a geometria é mais complexa do que uma mola linear, discretiza-se a geometria e a partir de cada componente (elemento) da estrutura discretizada e do conhecimento das propriedades de matérias que a constituem, obtém-se a rigidez do elemento. Os elementos são conectados pelos vértices, chamados nós, formando a estrutura contínua discretizada.
Matematicamente, com a rigidez de cada elemento e conhecendo-se os movimentos de cada nó, chamados de graus de liberdade (GDL) ou, em inglês, Degrees of Freedom (DOF), forma-se uma matriz de rigidez que representa a rigidez da estrutura de geometria complexa.
Na figura 2, que representa rigidez global, N é o número do grau de liberdade.
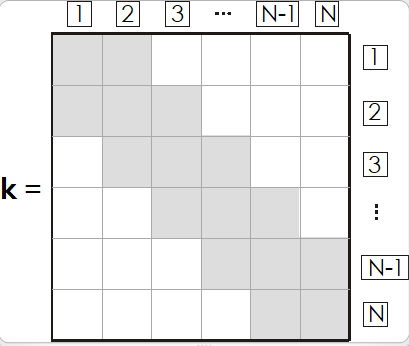
Figura 2: Matriz de rigidez global da estrutura
Pode-se, desta maneira, escrever a relação em forma matricial, entre esforço externo, rigidez e deslocamento. Onde:

{ F } – vetor de esforços externos
[ K ]– rigidez global
{ u }– vetor dos deslocamentos
Neste problema, os deslocamentos são os valores desconhecidos (as incógnitas) do problema, e, na sequência, um procedimento de solução de sistemas de equações (um solver) é utilizado e os deslocamentos de cada nó são calculados. A partir dos deslocamentos obtêm-se as tensões, deformações, reações de apoio e outras respostas que buscam os analistas.
Método dos Elementos Discretos (DEM)
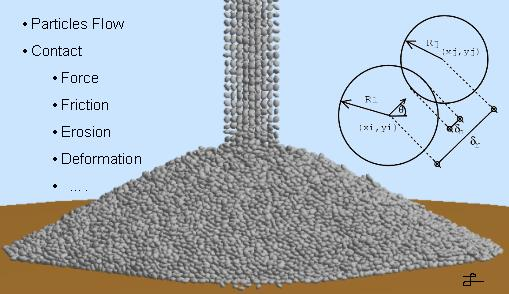
Um método dos elementos discretos ou método dos elementos distintos (DEM – Discrete Element Method ou Distinct Element Method) é, de fato, algum método de uma família de métodos para calcular o movimento e o efeito de um grande número de partículas pequenas (discretas).
O método dos elementos discretos está relacionado à dinâmica molecular, mas se diferencia devido à inclusão de graus de liberdade (movimentos) de rotação, contato entre os elementos discretos e, frequentemente, geometrias complexas usadas para defini-los.
Há diferentes ramificações da família, como o método dos elementos distintos proposto por Cundall em 1971, o método dos elementos discretos generalizados (Willians, Hocking e Mustoe) em 1985, o método de deformação descontínua (Shi, 1992) e o método dos elementos finitos discretos desenvolvido simultaneamente por diferente equipes (por exemplo Munjiza e Owen). O método geral foi desenvolvido originalmente por Peter Cundall em 1971 para solucionar problemas com geomecânica (rochas).
Utilize Ansys Rocky para simulações utilizando o método dos elementos discretos.
Em poucas palavras uma simulação com o DEM é iniciada com a geração de um modelo onde resultam em orientação espacial e velocidade inicial para todas as partículas. As forças que atuam em cada partícula são calculadas partir das condições iniciais, e das leis da física relevantes (mecânica Newtoniana) e contato. O resultado, um novo arranjo das partículas, pode ser visualizado num software de visualização projetado para este fim (um pós-processador).
Correntemente, o DEM é aceito como um método de análise eficaz para simular problemas de engenharia que envolve grãos e materiais descontínuos como escoamento granular e geomecânica. Os recentes avanços na capacidade de solução de grandes sistemas de equações seja por desenvolvimento e redução de preços dos computadores, processamento paralelo e dos algoritmos numéricos, permitem a solução de problemas computacionalmente intensivos, com número grande de partículas.

Figura 3 – Representação do contato entre partículas (formato esférico).
A premissa fundamental do método é que o material consiste de partículas discretas, separadas. Estas partículas podem ter diferentes formas e propriedades como, por exemplo: grãos, pedras, areia, toner, comprimidos, açúcar.
As indústrias que tipicamente usam o DEM são: agrícola, alimentos, química, mineração, farmacêutica, metalurgia do pó, engenharia civil, indústria de óleo e gás, processamento de minérios.
Método dos Volumes Finitos (FVM)
O método de volumes finitos (FVM – Finite Volume Method) foi introduzido na década de 1970 por McDonald, MacCormack e Paullay e, historicamente, tem sido o método preferido pelos cientistas e engenheiros que trabalham com a mecânica de fluidos, embora ele, FVM, não se limite apenas a solução de problemas de mecânica de fluidos.
Correntemente, o método dos volumes finitos é usado para resolver problemas da mecânica dos fluidos alguns deles considerados complexos como os que envolvem fluxos multifásicos, reativos, ou fortemente turbulentos. Na prática, o FVM mostrou-se o método mais eficaz no cálculo e solução de diferentes problemas de mecânica dos fluidos.
Para entender melhor sobre o método dos volumes finitos, assista o curso grátis Método dos Volumes Finitos para CFD – Parte I, ministrada pelo professor Clovis Maliska, especialista em CFD.
Considere-se que no método de volumes finitos há a decomposição (discretização) do domínio contínuo em pequenos volumes, chamados de volumes de controle (VCs), onde as variáveis são calculadas e armazenadas nos nós ou no centro do volume. Estes volumes de controle são conectados por estes nós e definem uma grade numérica chamada malha ilustrada na Figura 1. A figura 2 mostra os nós (ali chamados Nodos) nos vértices e centro dos volumes.
No Método dos Volumes Finitos usa-se a ideia de observação de Euler, isto é, material flui por um volume de controle fixo. A partir dos valores calculados nos nós e centros dos volumes de controle obtém-se uma solução que é transportada para o restante do domínio.

Figura 4: Malhas superficiais coloridas pela razão de aspecto da célula. Disponível em https://blog.pointwise.com
Os princípios de conservação da massa, momentum (quantidade de movimento) e energia, são a base da modelagem matemática no Método dos Volumes Finitos para a mecânica do contínuo. Por definição, estes princípios são respeitados pelas equações montadas a partir da discretização do contínuo que se realiza neste método. De forma geral o FVM envolve os seguintes passos:
- Decompor o domínio em volumes de controle;
- Formular as equações integrais de conservação para cada volume de controle;
- Aproximar numericamente as integrais;
- Aproximar os valores das variáveis nas faces e as derivadas com a informação das variáveis nodais;
- Montar e resolver o sistema algébrico obtido;
O sistema de equações é resolvido e como resultado obtêm-se respostas como pressão, temperatura e velocidade. Observe-se que é uma solução numérica aproximada. Um aspecto fundamental nos algoritmos de solução é o processo de decomposição de matrizes onde diversas técnicas têm sido desenvolvidas para aumentar a eficiência do uso de recursos computacionais e a velocidade da obtenção de resultados.
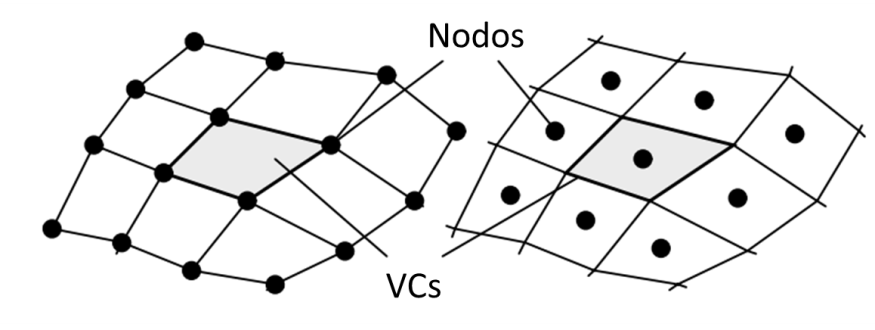
Figura 5: Nós nos vértices dos VCs (esquerda) e nós nos centros dos VCs (direita) para uma grade quadrilátera.
Outros métodos numéricos usados para solução de problemas de engenharia:
Método dos Elementos de Contorno (BEM)
O método dos elementos de contorno (BEM – Boundary Element Method) é um método computacional para a solução de sistemas de equações diferenciais, formuladas em forma integral. É aplicado em diversas áreas da engenharia, como por exemplo, em mecânica dos fluidos, acústica, eletromagnetismo e mecânica de fraturas.
No BEM o contorno do domínio em estudo é discretizado (dividido em elementos). Isto, em muitos casos, reduz drasticamente o tamanho do problema, além de ser mais simples a implementação de pré-processadores (geradores de geometria e de malha). Uma vez encontrada a solução no contorno, no estágio de pós-processamento, as equações integrais são novamente usadas para calcular numericamente a solução em qualquer ponto no interior do domínio envolvido pelo contorno.
Método das Diferenças Finitas (FDM)
Em matemática, os métodos de diferença finita (FDM – Finite Difference Method) são métodos numéricos para resolver equações diferenciais, aproximando-os com equações de diferença, nas quais as diferenças finitas se aproximam das derivadas. Os FDMs são, portanto, métodos de discretização. O método de diferenças finitas depende da discretização de uma função em uma grade (“grid”).
Método de Lattice-Boltzmann
Lattice Boltzmann é frequentemente considerado como um solver numérico da equação de Boltzmann. A equação de Boltzmann é o análogo da equação de Navier-Stokes a nível molecular, onde descreve a dinâmica espaço-temporal de uma quantidade estatística chamada função de distribuição de probabilidade, que é definida em espaço de fase de seis dimensões. O número de fenômenos físicos cobertos pelo modelo neste nível molecular de descrição é maior do que no nível hidrodinâmico da equação de Navier-Stokes.
A simulação computacional utiliza esses métodos numéricos em diferentes indústrias para auxiliar engenheiros a solucionar problemas. Para aplicar a simulação em seu negócio, entre em contato com a ESSS.

