Compósitos: modelagem de materiais de elevada resistência e rigidez
A utilização de materiais compósitos (ou simplesmente compósitos) vem ganhando popularidade nas últimas décadas, especialmente nas indústrias automotiva e aeroespacial. Entre as vantagens dos compósitos sobre os metais convencionais estão a elevada razão resistência mecânica/massa aliada a excelente resistência a corrosão, conformabilidade e durabilidade. Na sua forma mais simples os compósitos são avançados materiais de engenharia formados por um ou mais materiais constituintes. Estes materiais possuem propriedades físicas significativamente diferentes e, quando combinados, resultam em propriedades globais de elevada resistência e rigidez. A figura 1 rascunha o que vem ser uma estrutura compósita laminada. Um material matriz é utilizado como material base homogêneo, formando o núcleo da camada de material compósito. Fibras de reforço embutidas ou coladas são responsáveis pela anisotropia da estrutura e são utilizadas para prover a rigidez direcional. Um material compósito na sua forma laminar é usualmente conhecido como “layer” ou “ply”, o que significa “camada” ou “compensado”. Finalmente, um laminado é uma pilha de lâminas aglomeradas em direções arbitrárias, e são tipicamente referenciadas como compósitos do tipo “lay-up”.

Figura 1 – Esquema de uma estrutura laminar compósita.
O ANSYS oferece uma variedade razoável de ferramentas para efetivamente modelar estruturas de compósitos, entre as quais podemos encontrar a definição “Shell Section”, que prontamente define o número de camadas a ser utilizada, sua orientação e propriedades de material; vários tipos de vigas, “Layered Shells”, sólidos e elementos do tipo Solid-Shell, além das teorias de falha clássicas que podem ser utilizadas para predizer a probabilidade de haver falha estrutural. A um nível global (laminado), o usuário pode verificar as deflexões da estrutura, cargas de flambagem críticas, além de freqüências naturais e modos de vibrar. Ao nível laminar (da camada), tensões de cisalhamento interlaminar (entre as lâminas) podem ser estudadas para verificar a possibilidade de “delaminação” no compósito. Semelhantemente, é possível acessar a distribuição de tensões na interface matriz/fibra, ao nível da matriz. O primeiro passo no modelamento da estrutura de compósito no ANSYS é definir a arquitetura da camada (número de camadas, material das mesmas e sua orientação). A ferramenta básica fornecida pelo ANSYS para definir um compósito do tipo “Layup” é chamada “Shell Section”, a qual permite definições de lâminas “Layer-Wise”, “Tapered Sections”, “Shell Offsets”, rigidez de cisalhamento transversal, massa adicionada, entre outros. Há dois tipos principais de “Shell Section” no ANSYS: “Regular Shell Section” e “Pre-Integrated Shell Section”. A primeira delas, mostrada na Figura 2, permite ao usuário especificar o laminado a um nível camada a camada, paralelamente à espessura das camadas, tipo de material, orientação das fibras e quantidade dos pontos de integração ao longo da espessura.

Figura 2 – “Regular Shell Section” no ANSYS.
A “Pre-Integrated Shell Section” (Figura 3) requer as matrizes do laminado compósito ([A], [B] e [D]), as quais representam as relações entre força/momento e deformação/curvatura para o elemento, e deve ser calculado fora do ambiente ANSYS. É importante notar que se uma seção do tipo “Pre-Integrated Section” for usada, então as matrizes podem representar um número ilimitado de camadas, mas resultados (pós-processamento) detalhados em cada camada não poderiam ser obtidos uma vez que informações individuais para cada camada não fazem parte dos dados de entrada.

Figura 3 – “Pre-integrated shell section” no ANSYS
Uma vez que o laminado compósito tenha sido definido, é necessário escolher o tipo de elemento a ser utilizado durante a simulação. De uma maneira geral, as seguintes hipóteses são assumidas com relação ao modelamento de materiais compósitos: há uma união perfeita entre as camadas do laminado, o que implica que as lâminas não podem deslizar uma em relação às outras; o campo de deslocamento apresenta ao menos continuidade de curvatura através da espessura dos laminados. A teoria clássica dos laminados (CLT – Classical Laminate Theory) e a teoria de deformação cisalhante de primeira ordem (FSDT – First Order Shear Deformation Theory) são usadas nas formulações elementares. O ANSYS oferece uma rica variedade de elementos para modelamento de compósitos a diferentes níveis de precisão. O mais comum destes elementos é mostrado na Tabela 1.

Tabela 1 – Elementos ANSYS disponíveis para modelamento de compósitos.
Elementos de viga (1-D) usam o FSDT e são capazes de obter deformações finitas e assim modelar uma vasta amplitude de materiais (tais como elásticos, plásticos, visco-elásticos, etc.). Elementos de casca compósitos 2D – Layered Shell) são também baseados na teoria FSDT, mas são capazes de modelar grandes rotações e deformações finitas tanto quanto os tipos de comportamento apenas de membrana (ou seja, negligenciando a resistência ao cisalhamento transversal). Se é necessário obter precisão superior nos resultados de tensão e deformação, então o usuário poderá escolher os sólidos compósitos (Layered Solids) e os elementos do tipo Solid-Shell (Solid Shell Elements) – elementos 3D – a fim de modelar o laminado compósito. Elementos do tipo “Solid-Shell” são formulados utilizando a teoria de casca, mas a espessura é explicitamente definida em três dimensões (3D) da mesma forma como elementos sólidos regulares. Estes elementos permitem uma boa representação das tensões cisalhantes interlaminares a um custo computacional menor que os elementos sólidos regulares. A fim de efetuar uma comparação do desempenho dos elementos sólidos (SOLID185, SOLID186) contra os elementos do tipo “Solid-Shell” (SOLSH190), uma análise modal e de flambagem de um painel compósito foi executada utilizando ambos os tipos de elementos. O modelo do painel compósito, mostrado na Figura 4, consiste de uma casca compósita, reforçada com membranas verticais (Stringer Web) e um flange horizontal (Stringer Flange). Em primeiro lugar, as frequências naturais do laminado são extraídas para que observemos o comportamento característico da vibração livre-livre, seguidas de uma análise de flambagem para determinar a flambagem primária da casca.
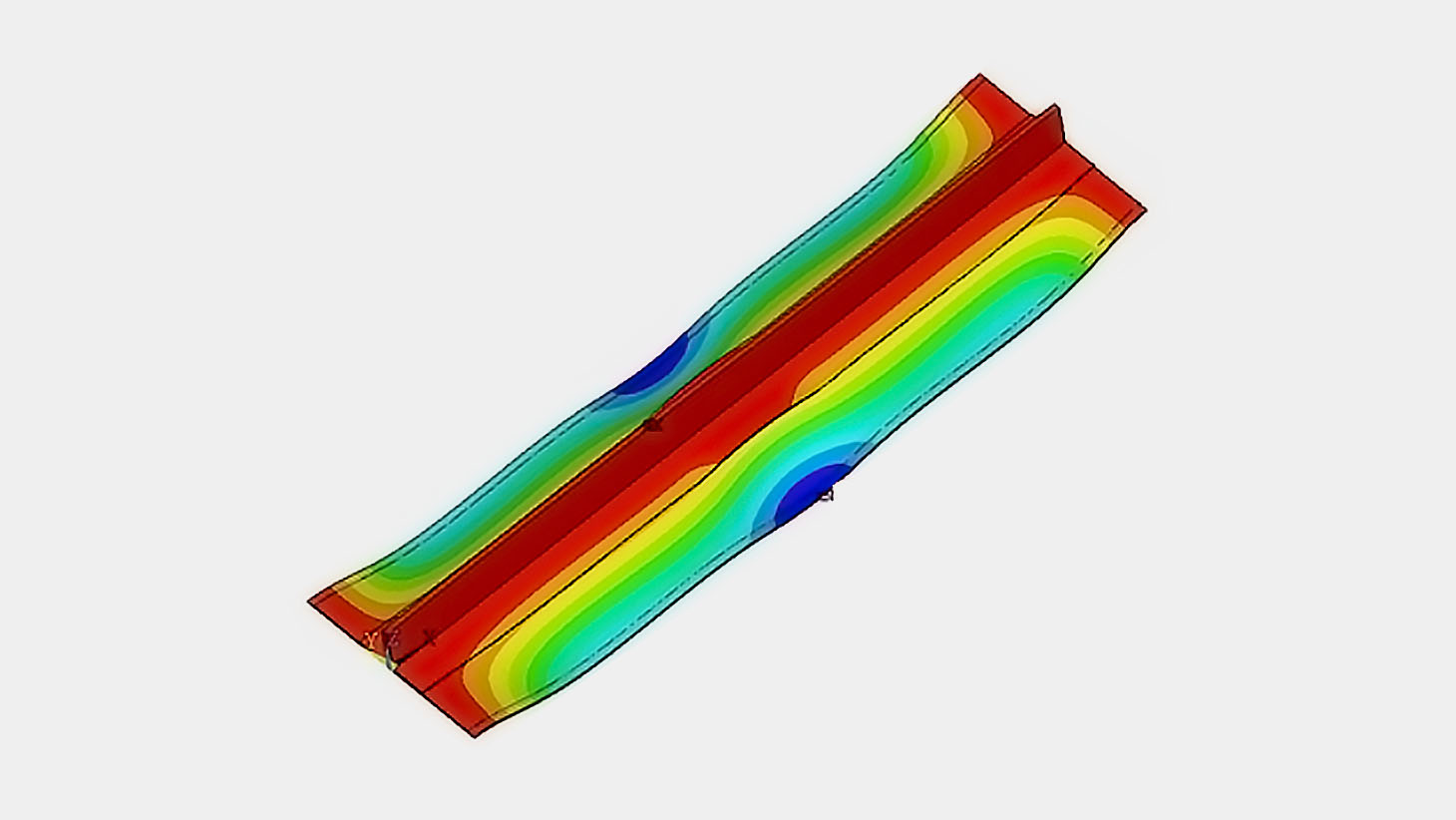
A Figura 5 mostra o gradiente de cores para o primeiro modo de vibrar, onde é observado que ambos os elementos predizem o mesmo modo de vibrar quase identicamente, enquanto que o modelo com elementos SOLSH190 superestima a primeira frequência natural em apenas 2.89%.

Figura 5 – Gradiente de cores do primeiro modo de vibrar.
A Figura 6 mostra o gradiente de cores que representam o deslocamento vertical do painel sob aplicação de uma carga compressiva de 30kN, onde é observado que ambos os elementos predizem a ocorrência de flambagem primária na mesma região e aproximadamente da mesma magnitude.

Figura 6 – Deslocamento vertical sob carregamento de 30kN.
Finalmente, a Figura 7 mostra a deformação vertical contra a carga compressiva da estrutura compósita. Os gráficos mostram que ambos os modelos predizem o início da flambagem primária de maneira quase idêntica, enquanto que o modelo utilizando o SOLSH190 começa por “enrijecer” após o início dos primeiros sinais de flambagem. A despeito deste aparente aumento de rigidez, o modelo utilizando SOLSH190 é capaz de predizer a resposta da estrutura pós-flambagem do painel além do que seria possível com elementos sólidos SOLID186, mostrando a versatilidade ao enfrentar os problemas de compósitos. Não é possível fornecer uma extensiva e detalhada descrição de todas as funcionalidades do modelamento de estruturas compósitas em apenas um artigo. Contudo, espera-se que algumas das melhores características deste tipo de análise tenham sido expostas aos usuários ANSYS, destacando a facilidade na utilização e os vários tipos de análises que podem ser executadas com a ajuda desta ferramenta. Embora um exemplo bem simples tenha sido apresentado, o ANSYS possui uma vasta quantidade de ferramentas para o modelamento de estruturas compósitas, a níveis locais e globais. Com o tempo, estas características continuarão a evoluir, aperfeiçoando-se e tornando-se cada vez mais amigáveis aos analistas de CAE, responsáveis pela avaliação da integridade estrutural de componentes e montagens, revisão de projetos ou simplesmente por estudos paramétricos ou de otimização de arquiteturas laminares compósitas.


Figura 7 – Deslocamento versus carregamento.
Jean Paul Kabche, ESSS

